I have wondered how the closed form for the sum of squares for the first n natural numbers was derived Given the formula for the sum 1^22^2n^2= n(n1)(2n1)/6 I learned to prove its correctness using mathematical induction However, I never The number of subsets of a set S with n elements is 2^n So using this information, knowing that the subset S ( S is a subset if itself) is not a proper subset, I can deduce that the total number of proper subsets is 2^n 1 since all other subsets are not equal to S and therefore must be proper subsets by definitionSum of n, n², or n³ n n are positive integers Each of these series can be calculated through a closedform formula The case 5050 5050 5050 ∑ k = 1 n k = n ( n 1) 2 ∑ k = 1 n k 2 = n ( n 1) ( 2 n 1) 6 ∑ k = 1 n k 3 = n 2 ( n 1) 2 4

Sums Of Consecutive Natural Numbers Ppt Video Online Download
N(n-1)/2 formula
N(n-1)/2 formula-The major research on series of numbers like the Fermat numbers $ (2^{2^n} 1) $ or the Mersenne numbers $ (2^n1) $ is done on finding prime numbers (numbers that their only divisors are 1 and the number itself, 1 is not prime number byThus, we see that 123(n2)(n1)n = n(n1)/2 For our second look at deriving this formula, we will take a geometric approach It should also be noted that we will make use of notation associated with the triangular numbers The triangular numbers are a set of numbers that result from adding the first n consecutive natural numbers



Untitled Document
2DIETHYLAMINONETHYLNOCTYLACETAMIDE HYDROCHLORIDE 2DIETHYLAMINONETHYLNOCTYLACETAMIDE HYDROCHLORIDE Molecular Weight Linear Formula C16H35ClN2O Product Number The way the items are ordered now you can see that each of those pairs is equal to N (N11 is N, N22 is N) Since there are N1 items, there are (N1)/2 such pairs So you're adding N (N1)/2 times, so the total value is N* (N1)/2 sum_(i=1)^n (1i/n)(2/n) = (3n1)/n lim_(n rarr oo)sum_(i=1)^n (1i/n)(2/n) = 3 > Let S_n = sum_(i=1)^n (1i/n)(2/n) S_n = sum_(i=1)^n (2/n(2i)/n^2) S_n = 2/n
Get the list of basic algebra formulas in Maths at BYJU'S Stay tuned with BYJU'S to get all the important formulas in various chapters like trigonometry, probability and so on 21 For the proof, we will count the number of dots in T (n) but, instead of summing the numbers 1, 2, 3, etc up to n we will find the total using only one multiplication and one division!Shows up which is the value in the denominator
The formula n (n − 1) / 2 for the number of pairs you can form from an n element set has many derivations, even many on this site One is to imagine a room with n people, each of whom shakes hands with everyone else If you focus on just one person you see that she participates inS(n) of the first npositive integers is equal to n(n1)/2N (n 1) 1 The formula 1 23n= is true for all integers n > 1 Use this 2 fact to solve each of the following problems a) If k is an integer and k > 2, find a formula for the expression 12



Approximations For The Factorial Function




Art Of Problem Solving
Use integration by parts to prove the reduction formulaint (x^2 a^2)^n dx = (x(x^2 a^2)^n)/(2n1) 2na^2/(2n 1) int(x^2 a^2)^(n1) dxEnter explicit rule into y 1 2nd Graph to view table f(f(n) = 512 In 10 hours, there will be 512 bacteria 5 You are making a house of cards similar to the one shown a) Write an explicit rule that can be used to find the number of cards in the nth row 6The first question is easier to answer If you know the mean value of the data from somewhere else, use the n version but if you are calculating the mean value of the data from the data itself (by summing the data & dividing by n or using the button on the calculator) use the n1 version



Untitled Document




Sum Of Squares Of First N Numbers
Ask Question Asked 6 years, 8 months ago Active 1 year, 1 month ago Viewed 10k times 42 16 $\begingroup$ I heard Gauss's primary school teacher gave some busywork to his class to add all the numbers between 1 and 100 up Gauss immediately wrote 5050Recursive Formulas Definition A recursive formula is defined on the set of integers greater than or equal to some number m (usually 0 or 1) The formula computes the nth value based on some or all of the previous n 1 valuesLet us write the multiplies out in full 7 × 6 × 5 × 4 × 3 × 2 × 14 × 3 × 2 × 1 = 7 × 6 × 5 That was neat The 4 × 3 × 2 × 1 "cancelled out", leaving only 7 × 6 × 5 And 7 × 6 × 5 = 210 So there are 210 different ways that 7 people could come 1 st, 2 nd and 3 rd Done!
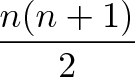



Techniques For Adding The Numbers 1 To 100 Betterexplained
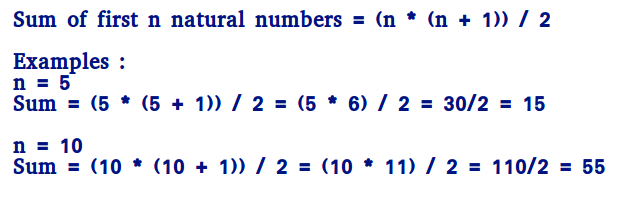



Program To Find Sum Of First N Natural Numbers Geeksforgeeks
Explanation S = n(n 1) 2 S = n2 n 2 2S = n2 n n2 n −2S = 0 using the quadratic formula for ax2 bx c = 0, n = −b ± √b2 −4ac 2aProof of x ^n algebraically Given (ab) ^n = (n, 0) a ^n b ^0 (n, 1) a ^(n1) b ^1 (n, 2) a ^(n2) b ^2 (n, n) a ^0 b ^n Here (n,k) is the binary Add the two equations, term by term;



How To Calculate 1 2 3 4 5 6 7 8 9 10 Quickly Quora




n Formula
To do this, we will fit two copies of a triangle of dots together, one red and an upsidedown copy in green Eg T (4)=1234The formula is 7!(7−3)!(a) Find a formula for the nth triangular number, where {eq}S_n=123 \cdots n {/eq} (b) For what values of {eq}n {/eq} is {eq}S_{n} {/eq} even?



Establish A Formula For 1 1 4 1 1 9 1 1 N 2 Stumbling Robot




A Mathematical Ode To Euler Proving Euler S Identity By James D Nickel Copyright E I 1 0 Or E I Ppt Download
2S n =n(2a(n1)d) S n =n(2a(n1)d)/2 The first term in the series is a, and the last one is a(n1)d, so we can say the sum of the series is the first term plus the last term multiplied by the number of terms divided by 2N be de ned as I n=S ˇ~2 0 sinnxdx for n=1;2 1Show that the following formulas are valid Hint sine reduction formula and induction I 2n = S ˇ~2 0 sin2nxdx= 1⋅3⋅5 (2n−1) 2⋅4⋅6 (2n) ˇ 2 for n=1;2 (1) I 2n1 = S ˇ~2 0 sin2n1 xdx= 2⋅4⋅6 (2n) 3⋅5⋅7 (2n1) for n=1;2 (2) The key to proving the above formulas is the followingSolve your math problems using our free math solver with stepbystep solutions Our math solver supports basic math, prealgebra, algebra, trigonometry, calculus and more




1 2 2 3 3 4 N N 1 Formula Novocom Top




Explanation Of Vasicek Model Bionic Turtle
Did Gauss find the formula for $123\ldots(n2)(n1)n$ in elementary school? Stack Exchange network consists of 177 Q&A communities including Stack Overflow, the largest, most trusted online community for developers to learn, share their knowledge, and build their careers Visit Stack ExchangeThe nth partial sum is given by a simple formula ∑ k = 1 n k = n ( n 1 ) 2 {\displaystyle \sum _{k=1}^{n}k={\frac {n(n1)}{2}}} This equation was known to the Pythagoreans as early as the sixth century BCE 5




Formulas N N 1 K 1




The Taylor Formula Online Presentation
Use the formula S = n (n 1)2 to find the sum of 1 2 3 385= Use the formula S = n2 to find the sum of 1 3 5 915 = (Hint To find n, add 1 to the last term and divide by 2)\left ( {n 2} \right)! n 1 and n 2 are integers where n 2 > n 1 It was later found that n 2 and n 1 were related to the principal quantum number or energy quantum number This formula works very well for transitions between energy levels of a hydrogen atom with only one electron



Prove By Induction A Formula For The Sum From 1 To Of Nkxn Stumbling Robot




Permutation Formula Programmer Sought
Until the expression ( n − 2)!Download Page POWERED BY THE WOLFRAM LANGUAGE Related Queries (integrate 1/n^2 from n = 1 to xi) (sum 1/n^2 from n = 1 to xi) bass guitars (consumer products) (integrate 1/n^2 from n = 1 to xi) / (sum 1/n^2 from n = 1 to xi) LOGO repeat 33 backward 80 forward right 11 left 71Each term is n 1, so 2S = (n 1) (n 1) (n 1) = n(n 1) Divide by 2 S = n(n 1) 2




Formula For The Sample Size Determination N N Population Young Download Scientific Diagram




Sums Of Consecutive Natural Numbers Ppt Video Online Download
In mathematics, the binomial coefficients are the positive integers that occur as coefficients in the binomial theoremCommonly, a binomial coefficient is indexed by a pair of integers n ≥ k ≥ 0 and is written () It is the coefficient of the x k term in the polynomial expansion of the binomial power (1 x) n, and is given by the formula =!!()!For example, the fourth power of 1 As @betlista has said, n (n1)/2 is the sum of the first (n1) numbers, that is 1 2 3 4 (n1) Now one might think that there is not much use for this formula, but when you do some research, you can find interesting uses for it @betlista has explained a few uses Here is a link which explains one usageI hope to help you understand why there are 2 formulas for the SD They are bith trying to do the same thing



Http Www Manhassetschools Org Cms Lib8 Ny Centricity Domain 710 Hw 85 key 9h Pdf




In The Formula T N A N 1 D Make N As The Subject
Step 2 Here, n is the number of items in the given data set That is, if you consider the above example data set, 1, 2, 4, and 8, the variable n's value is 4 Step 3 Just apply the variable value n in the formula to get the median ie Median = (n 1) / 2 It may seem very easy to see this formula since it is a very small set of dataN = 1/2 √ 961/4 Since a square root has two values, one positive and the other negative n 2 n 240 = 0 has two solutions n = 1/2 √ 961/4 or n = 1/2 √ 961/4 Note that √ 961/4 can be written as √ 961 / √ 4 which is 31 / 2 Solve Quadratic Equation using the Quadratic Formula 53 Solving n 2 n240 = 0 by the QuadraticComparing to above formula if we want to calculate sum up to n1, using the above formula we get n1 (n11)/2 That is n (n1)/2 Thus the required formula is n (n1)/2 186K views




Important Formulas In Combinatorics Mathoverflow




How To Sum The Integers From 1 To N 8 Steps With Pictures
Number Sequences In the sequence 2, 4, 6, 8, 10 there is an obvious pattern Such sequences can be expressed in terms of the nth term of the sequence In this case, the nth term = 2n To find the 1st term, put n = 1 into the formula, to find the 4th term, replace the n's by 4's 4th term = 2 × 4 = 8 Adding one more node has to establish N additional connections, and N * (N 1) / 2 N = (N^ 2 N 2N) / 2 = (N^ 2 N) / 2 = (N 1) * N / 2 This last line is exactly N * (N 1) / 2 with N replaced with N1, so the proof is good answered Mar 19 Samiur1 386kFactor n^21 n2 − 1 n 2 1 Rewrite 1 1 as 12 1 2 n2 − 12 n 2 1 2 Since both terms are perfect squares, factor using the difference of squares formula, a2 −b2 = (ab)(a−b) a 2 b 2 = ( a b) ( a b) where a = n a = n and b = 1 b = 1 (n1)(n− 1) ( n 1) ( n 1)




Binomial Expansion Formulas Derivation Examples




Derivation Formula Sum Of First N Squares Or Square Numbers 1 2 2 2 3 2 4 2 N 2 Youtube
I tried to compute it with the factorial expression for the binomial coefficients, but the second term already has n=1/2 and k=1, which makes the calculation for the binomial coefficient (n 1) weird, I thinkExamples of Simplifying Factorials with Variables Example 1 Simplify Since the factorial expression in the numerator is larger than the denominator, I can partially expand n! Binomial expansion with n=1/2 #1 gentsagree 96 1 Is it possible to do a binomial expansion of ?




Binomial Theorem Properties Terms In Binomial Expansion Examples Pdf




Gamma Function Wikipedia
Derivation of the formula in a way which is easy to understand It will also help student to remember the formula easily This is the foundation for next fewComparing to above formula if we want to calculate sum up to n1, using the above formula we get n1 (n11)/2 That is n (n1)/2 Thus the required formula is n (n1)/2 157K viewsPartial sum formula Partial sums More terms;



Combinations Calculator Ncr




Is There Any Elementary Formula For The Sequence Sum K 1 N Left 2k 1 Right Left Frac 1 2 Right K Mathematics Stack Exchange
Simple and best practice solution for n(n1)=2 equation Check how easy it is, and learn it for the future Our solution is simple, and easy to understand,N N 1 2 Formula Name rock n roller coaster ride photos ro river rock n roller coaster layout rock n roller coaster starring aerosmith romancing the stone blu ray rock n roller coaster inside rookie halo 3 odst wallpaper rock around the clock piano letters rock n roller coaster ride vehicle rock n roller coaster closing orlandoS = n/2 2 1 = 2 = a n / a n1 Summation of Cubes Formula
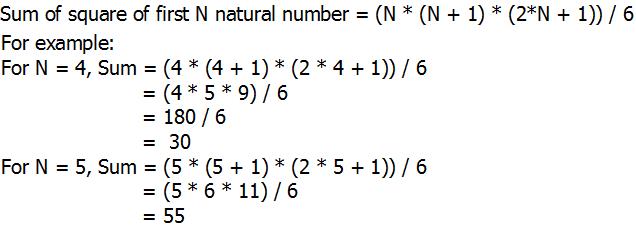



Python Program For Sum Of Squares Of First N Natural Numbers Geeksforgeeks



Binomial Expansion And Series A Level Maths Uptuition With Mr Will



1




Summations Cop 3502 Summations Why Do We Need




Moving Average Wikipedia



Untitled Document




Geometric Series Wikipedia



Search Q Summation Formulas Tbm Isch




1 2 2 3 3 4 N N 1 Formula Novocom Top




Sum Of N N Or N Brilliant Math Science Wiki
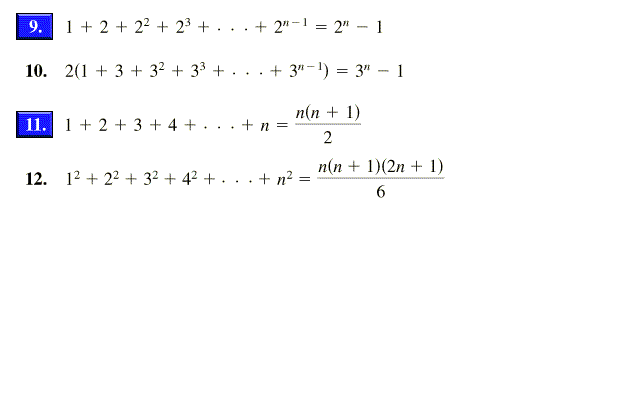



In Exercises 5 18 Use Mathematical Induction To Chegg Com




Factorial Calculator Solve N Inch Calculator



Jay S Corner 4




From Artin Prove The General Formula Of Discriminant Of X N Px Q For N 2 Mathematics Stack Exchange




1234n Formula




5 4 Mathematical Induction T



Is There Is Any Formula For 1 2 3 4 N And 1 2 2 2 3 2 N 2 Quora



The Science Behind Why Jeff Bezos S Two Pizza Team Rule Works Hcl




Answered I Proving A Formula Use Mathematical Bartleby




Proof Of Finite Arithmetic Series Formula By Induction Video Khan Academy




Prove By Induction Sum Of The First N Cubes 1 3 2 3 3 3 N 3 Youtube




Insertion Sort Analysis And Summation Notation Stack Overflow



Search Q 1 5e2 2b2 5e2 2b3 5e2 2b 2bn 5e2 Induction Tbm Isch




1 2 2 3 3 4 N N 1 Formula Novocom Top




How To Find Sum Of 1 N N 1 From N 1 To Infinity Quora
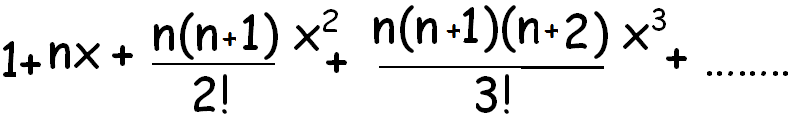



Binomial Expansion Formula For 1 Plus X Whole Power N
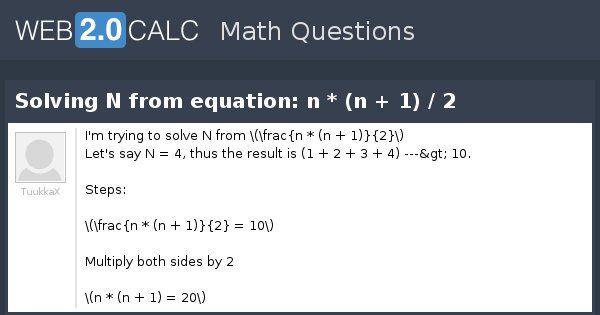



View Question Solving N From Equation N N 1 2




How To 12 Proof By Induction 1 3 2 3 3 3 N 3 N N 1 2 2 N 2 N 1 2 4 Prove Mathgotserved Youtube




Mathematical Induction Prezentaciya Onlajn



Faculty Math Illinois Edu Hildebr 213 Inductionsampler Pdf




n2 Formula Proof




The Catalan Numbers And Their Applications 1 2




Pdf Important Sum Formulas Omid Motahed Academia Edu




Different Formulas On Permutation Tutorsonnet
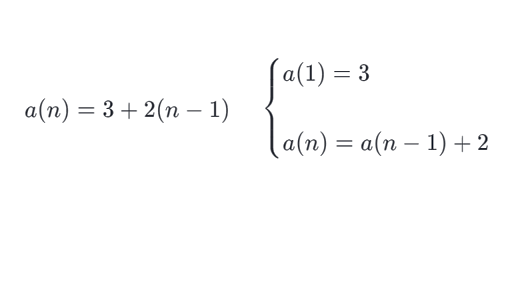



Intro To Arithmetic Sequence Formulas Algebra Article Khan Academy




The Formula Of The Sum Of First N Natural Numbers Is S N N 1 2 If The Sum Of First N Natural Brainly In




Factorial Of A Number N Formula Calculator
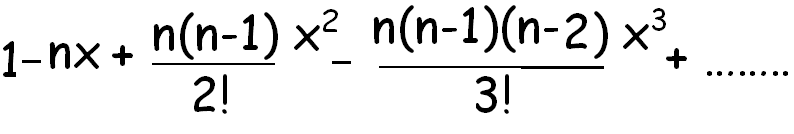



Find Binomial Expansion Of Rational Functions




1 2 2 3 3 4 N N 1 Formula Novocom Top




Prove The Formula I 1 N I 1 2 N N N 1 2 Chegg Com




Proof Of 1 2 2 2 Cdots N 2 N 3 3 N 2 2 N 6 Mathematics Stack Exchange




5 4 Mathematical Induction T



Python Challenges 1 Exercises Practice Solution W3resource



2 2 Some Summation Formulas
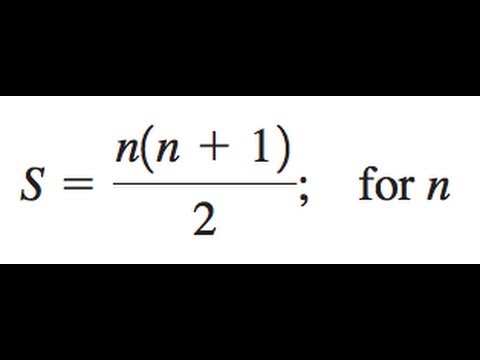



S N N 1 2 Solve For N Youtube




Ex 9 1 12 Write Five Terms Series A1 1 An An 1 N




Communication Channels How To Memorize Things Pmp Exam Cheat Sheets




How To Derive N 1 2 From 1 2 3 N N Quora




Use The Binomial Formula 1 Alpha N 1 N Alpha Chegg Com




Find A Formula For The Following 6 7 8 Chegg Com




How To Prove A Formula For The Sum Of Powers Of 2 By Induction Mathematics Stack Exchange




Let E N 1 N 1 N Follow The Following Chegg Com




Mathematics 1031 Formulas Interest Simple Interest A P 1 Rt




In Lecture We Came Up With Three Formulas For Chegg Com




Arithmetic Sequence Formula Chilimath




Problem 2 1 Show That For Any Positive Integer N We Chegg Com



n2 Formula Proof




Wallis Product Wikipedia




1234n Formula
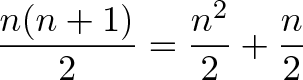



Techniques For Adding The Numbers 1 To 100 Betterexplained




Answered Then 9tm 1 Is Also Triangular Write Bartleby



Who Invented The Formula N N 1 2 Quora
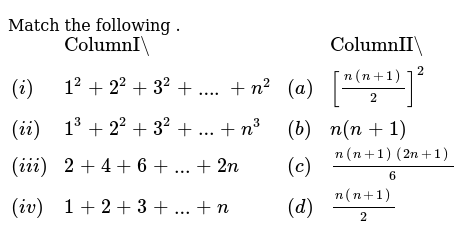



Mathod Of Induction 1 2 2 2 3 2 N 2 N N 1 2n 1 6




Faulhaber S Formula Wikipedia




5 4 Mathematical Induction T




Is This Modern Programming Interview Challenge S Solution Unreliable Stack Overflow




Pdf On The Diophantine Equation 2 N 1 3 N 1 X 2




4 Stirling 39 S Formula Is The Claim That N N O0 1 V2nn N E 34 In This Exercise We Will Homeworklib
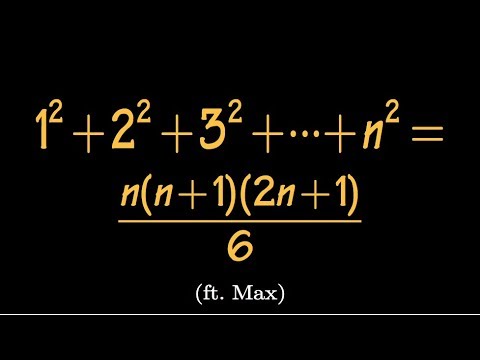



Find The Sum Of First N Squares Difference Equation Approach Ft Max Youtube




Answered And N 2n 1 N 1 3 5 13 The Bartleby




Find S N In Terms Of N Mathematics Stack Exchange
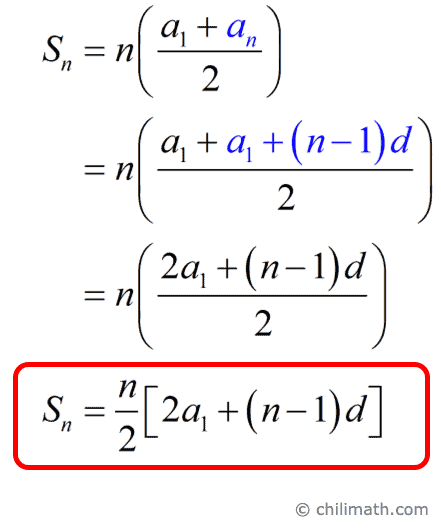



Arithmetic Series Formula Chilimath




Just Need Help Finding The A 3 N General Formula Chegg Com



1




What Is This Formula N N 1 2 Please Tell The Answer Brainly In



Finding The Sum Of Consecutive Numbers



0 件のコメント:
コメントを投稿