Find the volume of the region that lies under the paraboloid z = x 2 y 2 z = x 2 y 2 and above the triangle enclosed by the lines y = x, x = 0, y = x, x = 0, and x y = 2 x y = 2 in the x y x yplane (Figure 536) Solution First examine the region over which we need to set up the double integral and the accompanying paraboloidLet 𝒮 be the surface formed by the paraboloid z = 1x 2y 2, z ≥ 0, and the unit disk centered at the origin in the xy plane, graphed in Figure 1572, and let F → = 0, 0, z (This surface and vector field were used in Example 1563)Let Sbe the part of the paraboloid z= 7 x2 4y2 that lies above the plane z= 3, oriented with upward pointing normals Use Stokes' Theorem to nd ZZ S curlF~dS~ Solution Here is a picture of the surface S x y z The strategy is exactly the same as in#1 The

Find The Volume Of The Solid Bounded By The Plane Z 0 And The Paraboloid Z 1 X 2 Y 2 Use A Double Integral And Polar Coordinates Study Com
Enclosed by the paraboloid z=x^2+y^2+1
Enclosed by the paraboloid z=x^2+y^2+1-We can also write the cone surface as r = z r = z and the paraboloid as r 2 = 2 − z r 2 = 2 − z The lower bound for r r is zero, but the upper bound is sometimes the cone and the other times it is the paraboloid The plane z = 1 z = 1 divides the region into two paraboloide z=1x2y2 Publicado por tartari ( 2 intervenciones) el Gracias por contestarme, pues ya lo estaba haciendo así, pero no se porque razon la version de matlab que estoy utilizando no me muestra la grafica ni nada Además tambien debo realizar a continuacion las siguientes cosas Utilizando una parametrizacion




1 Find The Surface Area Of The Portion Of The Chegg Com
Solution to Problem Set #9 1 Find the area of the following surface (a) (15 pts) The part of the paraboloid z = 9 ¡ x2 ¡ y2 that lies above the x¡y plane ±4 ±2 0 2 4 x ±4 ±2 0 2 4 y ±4 ±2 0 2 4 Solution The part of the paraboloid z = 9¡x2 ¡y2 that lies above the x¡y plane must satisfy z = 9¡x2 ¡y2 ‚ 0 Thus x2 y2 • 9 WeAnswer to Find the area of the surface The part of the paraboloid z = 1 x^2 y^2 that lies above the plane z = 6 By signing up, you'll getLies beneath the paraboloid z = 1−x2 −y2 Solution The solid region E is 0 ≤ x ≤ 1, 0 ≤ y ≤ √ 1−x 2, 0 ≤ z ≤ 1−x2 −y So in cylindrical coordinates E 0 ≤ θ ≤ π2, 0 ≤ r ≤ 1, 0 ≤ z ≤ 1−r2 ZZZ E (x3 xy2)dV = Z π 2 0 Z 1 0 Z −r2 0 r3 cos3 θ (rcosθ)(r2 sin2 θ)rdzdrdθ = Z π 2 0 Z 1 0 Z −r2
Part Of The Elliptic Paraboloid Z X2 Y2 Which Can Be Generated By Stock Photo Alamy For more information and source, see on this link https Find The Area Of The Paraboloid Z 1 X 2 Y 2 That Lies In The First Octant Study Com For more information and source,Find the surface area of the part of the paraboloid z=16x^2y^2 that lies above the xy plane (see the figure below) The region R in the xyplane is the disk 05 (a) Find the center of mass of the solid S bounded by the paraboloid z = 4x2 4y2 and the plane z = 1 if S has constant density K Solution In cylindrical coordinates the region E is described by 0 ≤ r ≤ 1/2, 0 ≤ θ ≤ 2π, and 4r2 ≤ z ≤ 1 Thus, the mass of the solid is M = ZZZ E K dV = Z 2π 0 Z 1/2 0 Z 1 4r2 Krdzdrdθ = Kπ 8
Compute answers using Wolfram's breakthrough technology & knowledgebase, relied on by millions of students & professionals For math, science, nutrition, history2 Let T be the solid bounded by the paraboloid z= 4 x2 y2 and below by the xyplane Find the volume of T (Hint, use polar coordinates) Answer The intersection of z= 4 2x 22y and xyplane is 0 = 4 x2 y;ie x2 y = 4 In polar coordinates, z= 4 x2 y 2is z= 4 rSo, the volume is Z Z 4 x2 y2dxdy = Z 2ˇ 0 Z 2 0 4 r2 rdrd = 2ˇ Z 2 0 4r r3 2 dr8 Find the surface area of the paraboloid z = 4 x2 y2 that lies above the xyplane Solution For this problem polar coordinates are useful S = ZZ D s 1 @z @x 2 @z @y 2 dA = ZZ D p 14x2 4y2 dA = Z2ˇ 0 Z2 0 r p 14r2 drd = Z2ˇ 0 1 12 (14r2)3=2 2 d = ˇ 6 (17)3=2 1 9 Find the surface area of the surface z = 2 3(x 3=2 y3=2) for 0 6 x




Find The Surface Area Of The Paraboloid Z 1 X 2 Y 2 That Lies Above The Unit Circle In The Xy Plane Study Com



Math Help
Answer to Find the area of the paraboloid z = 1 x^2 y^2 that lies in the first octant By signing up, you'll get thousands of stepbystepFind The Volume Of The Solid Bounded By The Plane Z 0 And The Paraboloid Z 1 X 2 Y 2 Use A Double Integral And Polar Coordinates Study Com For more information and source, see on1 but if we instead describe the region using cylindrical coordinates, we nd that the solid is bounded
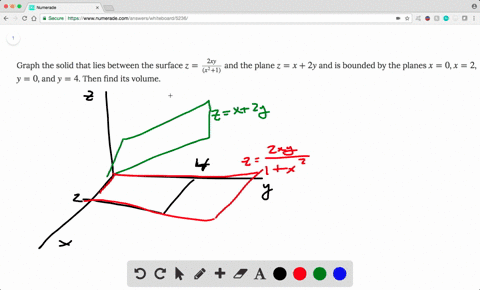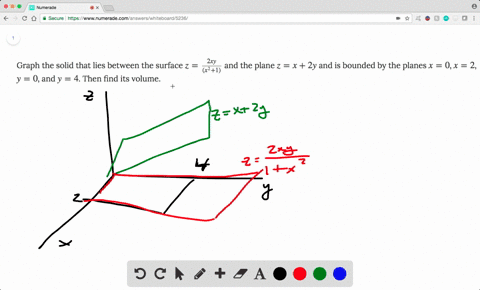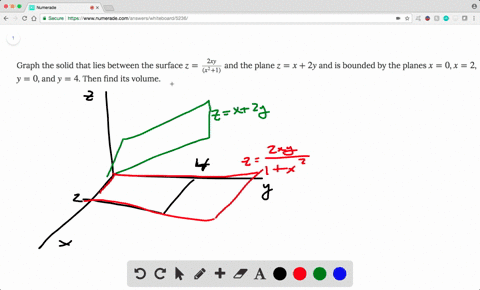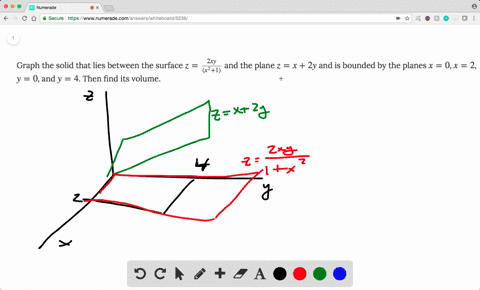



Solved Find The Volume Of The Solid Enclosed By T



Let S Be The Surface Of An Open Paraboloid Z Chegg Com
Compute answers using Wolfram's breakthrough technology & knowledgebase, relied on by millions of students & professionals For math, science, nutrition, historyFind The Volume Of The Solid Below The Paraboloid Z 4 X 2 Y 2 And Above The Region R R Theta 0 Leq R Leq 1 0 Leq Theta Leq 2 Pi Study Com Find The Volume Of The Solid Bounded By The Paraboloid Z 1 X 2 Y 2 And Below The Plane Z 1 Y Hint Equate The Z Values Study Com For more information and source,Compute the mass of the 3D region under above the xyplane and below the paraboloid z = 1x 2y 2 which has a density function ρ (x, y, z) = ρ 0 x 2 y 2 (Hint Convert to Spherical or Cylindrical coordinates) 7 Find the surface area of the segment of the paraboloid x



Double Integrals In Polar Coordinates Calculus Volume 3



Www Ualberta Ca Rjia Math215 Hwks Sol8 Pdf
Sis the surface of the solid bounded by the paraboloid z= 1 x2 y2 and the xyplane ZZ S FdS= ZZZ E div FdV div F= 6x 2 3y2 3y = 6(x2 y2) ZZZ E 6(x2 y2) dV = 6 Z 2ˇ 0 Z 1 0 Z 1 r2 0 r2rdzdrd = 6 Z 2ˇ 0 Z 1 0 r3 z 1 2r 0 drd = 6Where Eis the solid bounded below by the paraboloid z= x2 y2, above by the plane z= 4, and the planes y= 0 and y= 2 This integral can be evaluated as an iterated integral Z 2 2 Zp 4 x2 0 Z 4 x 2y f(x;y;z)dzdydx; $\begingroup$ @saulspatz Well we want to find the SURFACE area of part of the paraboloid that lies above the plane z = 4 And there is a formula to calculating surface area as shown in my first picture $\endgroup$ – Not Friedrich gauss Apr 5 ' at 426



15 3 Double Integrals In Polar Coordinates Mathematics Libretexts




Calc3 1001 By James Bardo Issuu
The 2 given surfaces are reflections of each other at the plane y=z because each of them mapped onto the other by interchanging between y and z Therefore their intersection contained inside that plane, and it is the curve given by Hence the per 0 Evaluate the volume of V ⊂ R 3, which is bounded by paraboloid z = 1 − x 2 − y 2 and the surface z = 1 − y, for z ⩾ 0 Attempt The desired volume goes like ∬ D ( 1 − x 2 − y 2 − ( 1 − y)) d x d y, where D is the projection of V on R 2 How do we determine D?(pts) Let S be the surface formed by the part of the paraboloid z = 1−x2−y2 lying above the xyplane Orient S so that the normal vector is pointing upwards Let F~ = xˆıyˆ 2(1−z)kˆ (i) Find the flux of F~ across S directly Solution We have dS~ = h2x,2y,1idxdy



Triple Integrals In Cylindrical And Spherical Coordinates




Find The Volume Of The Solid Bounded By The Paraboloid Z X 2 Y 2 And The Plane Z 9 Study Com
Assignment 8 (MATH 215, Q1) 1 Use the divergence theorem to find RR S F ndS (a) F(x,y,z) = x3 i 2xz2 j 3y2z k;4 Find the volume and centroid of the solid Ethat lies above the cone z= p x2 y2 and below the sphere x 2y z2 = 1, using cylindrical or spherical coordinates, whichever seems more appropriate Recall that the centroid is the center of mass of the solidS is the surface of the solid bounded by the paraboloid z = 4 − x2 − y2 and the xyplane Solution The divergence of F is




1 Find The Surface Area Of The Portion Of The Chegg Com



Surface Area
Solution The ux is the surface integral ZZ S F dS div F = 2xy2 3xy2 xy2 = 0 By the Divergence theorem ZZ S F d S = ZZZ E 0 dV = 0 2Solution If we put z = 0 in the equation of the paraboloid, we get x2 y2 = 1 This means that the plane intersects the paraboloid in the circle x2 y2 = 1, so the solid lies under the paraboloid and above the circular disk D given by x2 y2 ≤ 1 In polar coordinates D is given by 0 ≤ r ≤ 1, 0 ≤ θ ≤ 2π Since 1−x2 −y2 = 1−Find stepbystep solutions and your answer to the following textbook question Use cylindrical coordinates Evaluate triple integral (xyz)dV, where E is the solid in the first octant that lies under the paraboloid z=4x^2y^2



Users Math Msu Edu Users Bellro Lb2sp12homework S9 Pdf



What Is The Surface Area Of The Portion Of The Paraboloid Z 4 𝑥 2 𝑦 2 That Lies Above The Xy Plane Quora
Arrow_forward Buy Find launch Multivariable CalculusThe part of the paraboloid z = 1 x^2 y^2 that lies above the plane z = 2 Our Discord hit 10K members!Find the area of the surface The part of the paraboloid z = 4 − x 2 − y 2 z = 4 x^2 y^2 z = 4−x2 − y2 that lies above the xyplane Explanation A Explanation B Recall the formula for the area If



What Is The Volume Between Paraboloid Z X 2 Y 2 And Y X 2 Z 2 Quora




Notes Up To Ch7 Sec3
The surface S of the solid Ebounded by the hyperboloid x2 y2 z2 = 1 and the paraboloid z= 4 2x2 y, when z 0 ) Have a wonderful day!Figure 1 Region S bounded above by paraboloid z = 8−x2−y2 and below by paraboloid z = x2y2 Surfaces intersect on the curve x2 y2 = 4 = z So boundary of the projected region R in the x−y plane is x2 y2 = 4 Where the two surfaces intersect z = x2 y2 = 8 − x2 − y2 So, 2x2 2y2 = 8 or x2 y2 = 4 = z, this is the curve atParaboloid z = x2 y2 and below the half cone z = p x2 y2 Solution x = rcosθ, y = rsinθ, z = z, dV = rdrdθdz ZZZ E z dV = Z2π 0 Z1 0 Zr r2 zrdzdrdθ = Z2π 0 Z1 0 z2r 2 z=r z=r2 drdθ = Z2π 0 Z1 0 r3 2 − r5 2 drdθ = Z2π 0 r4 8 − r6 12 r=1 r=0 dθ = Z2π 0 1 24 dθ = π 12 Problem 5 Evaluate RRR E y dV, where E is enclosed by the




Finding The Surface Area Of The Paraboloid Z 1 X 2 Y 2 That Lies Above The Plane Z 4 Mathematics Stack Exchange




Let S Be Part Of The Paraboloid X2 Y2 That Lies Under The Plane Z Evaluate The Surface Inte Homeworklib
🎉 Meet students and ask top educators your questions Join Here! Solve the problem a student earned grades of c, a, b, and a in four different courses those courses had these corresponding numbers of credit hours 4, 5, 1, and 5 the grading system assigns quality points to letter grades as follows a = 4, b = 3, c = 2, d = 1, and f = 0 compute the grade point average (gpa) and round the result to two decimal places 340 350 875 218First week only $499!




Evaluate The Volume Bounded By Z 1 X 2 Y 2 And Z 1 Y Mathematics Stack Exchange




Finding The Surface Area Of The Paraboloid Z 1 X 2 Y 2 That Lies Above The Plane Z 4 Mathematics Stack Exchange
Use Stokes' Theorem to evaluate ∫ c F dr In each Case C is oriented counterclockwise as viewed from above 9 F(x, y, z) = xy i yz j zx k, C is the boundary of the part of the paraboloid z = 1 x 2 y 2 in the first octantProblem 3 Find the volume of the solid that lies between the paraboloid z = x2 y2 and the sphere x2 y2 z2 = 2 using 1 (15%) the cylindrical coordinate, and 2 (15%) the spherical coordinate Sol First we nd the intersection of the paraboloid and the sphere If (x,y,z) is on the intersection,It shows the paraboloid z = A x 2 B y 2 over the square domain1 ≤ x ≤ 11 ≤ y ≤ 1 If you change the domain to a disk, you will see the portion of the paraboloid for which 0 ≤ z ≤ 8 When you change A and B, the domain will change accordingly Here are a few things to think about




Find The Area Of The Paraboloid Z 1 X 2 Y 2 That Lies In The First Octant Study Com




Paraboloid Z 4 X 2 Y 2 Novocom Top
Order my "Ultimate Formulmznto/2SKuojN Hire me for private lessons https//wyzantcom/tutors/jjthetutorRead "The 7 Habits of Successful STParaboloid z = x 24y A trigonometric parametrization will often be better if you have to calculate a surface integral ( u;v) = Here we want x2 4y2 to be simple So x = 2r cos y = r sin will do better Plug x and y into z = x2 4y2 to get the zcomponent10 Use cylindrical coordinates to evaluate ZZ E (x 3 xy 2) dV where E is the solid in the rst octant the lies beneath the paraboloid z = 1x 2y 2 11 Evaluate ZZZ E xe x 2 y 2 z 2 dV where E is the portion of the unit ball x 2 y 2 z 2 ≤ 1 that lies in the rst octant 7



A Paraboloid Described By Z X 2 Y 2 On The Xy Plane And Partly Inside The Cylinder X 2 Y 2 2y How
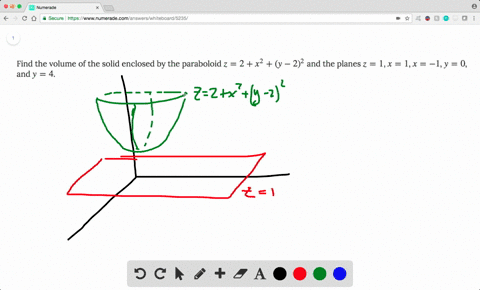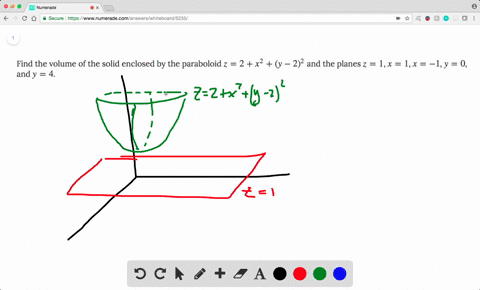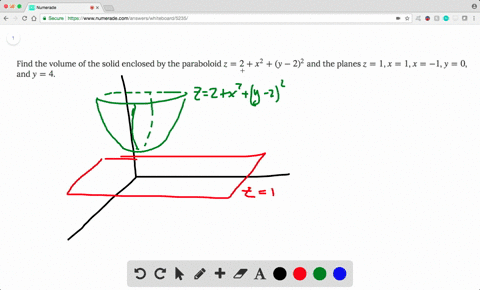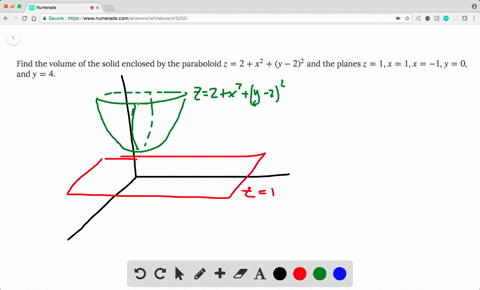



Solved Find The Volume Of The Solid Enclosed By T
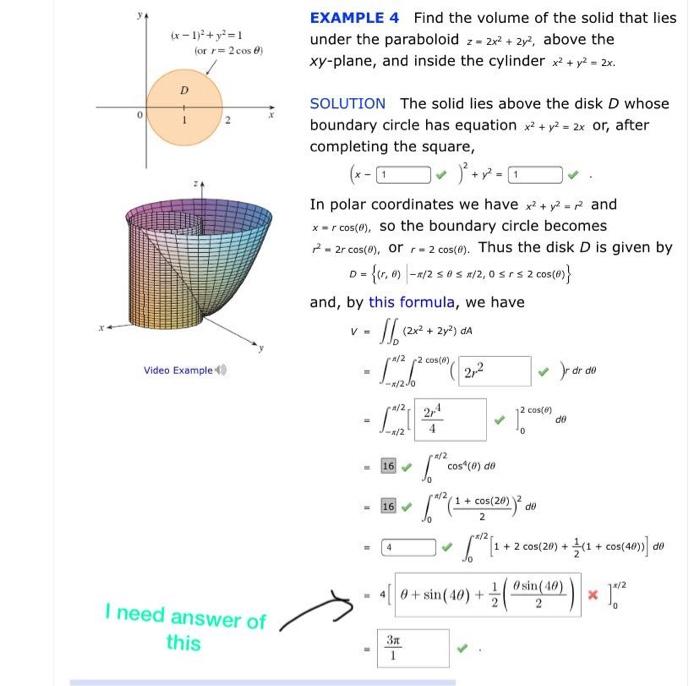
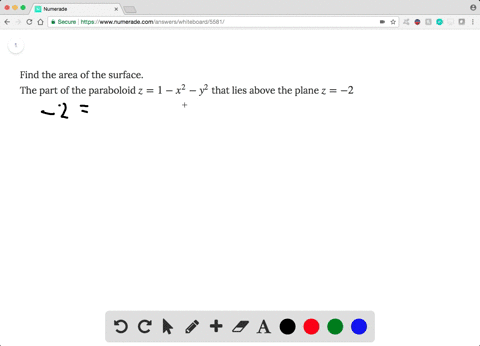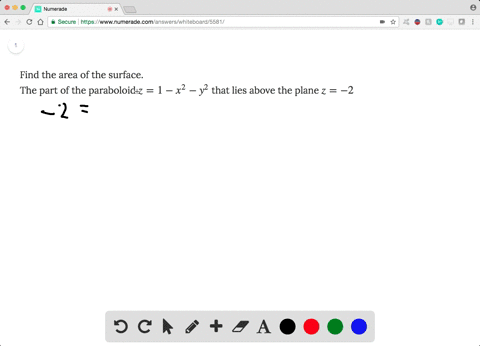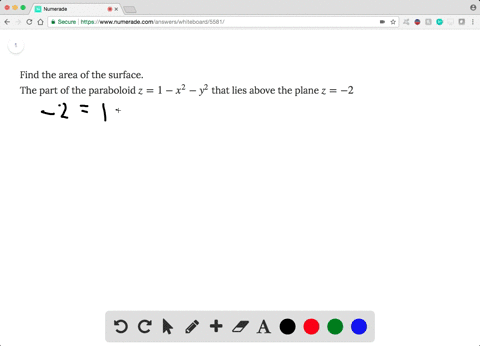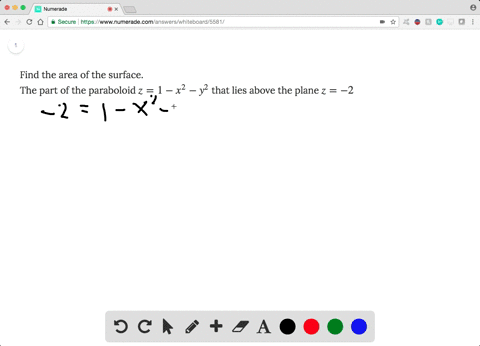
Problem 3 Let S be the boundary of the solid bounded by the paraboloid z = x2 y2 and the plane z = 4, with outward orientation (a) Find the surface area of S Note that the surface S consists of a portion of the paraboloid z = x2 y2 and a portion of the plane z = 4 Solution Let S1 be the part of the paraboloid z = x2 y2 that liesThe part of the paraboloid z = 1 – x 2 – y 2 that lies above the plane z = –2 more_vert Find the area of the surface 5 The part of the paraboloid z = 1 – x 2 – y 2 that lies above the plane z = –2 close Start your trial now!132 13 MULTIPLE INTEGRALS Example Find the volume of the solid that lies under the paraboloid z = x2 y2, above the xyplane, and inside the cylinder x2 y2 = 2x Completing the square, (x 1)2 y2 = 1 is the shadow of the cylinder in the xyplane Changing to polar coordinates, the shadow of the cylinder is r2 = 2rcos or r = 2cos , so




Finding The Surface Area Of The Paraboloid Z 1 X 2 Y 2 That Lies Above The Plane Z 4 Mathematics Stack Exchange



Search Q Paraboloid Equation Tbm Isch
Example Find the volume of the solid D bounded by the paraboloid S z = 25−x2 −y2 and the xyplane Solution The paraboloid S z = 25 − x2 − y2 intersect the xyplane p z = 0 in the curve C 0 = 25−x2 −y2, which is a circle x2 y2 = 52 So the shadow R of the solid D after projecting onto xyplane is given by the circular disc R = {(x,y) x2 y2 ≤ 52}, in polar coordinates is Find the volume of the region that lies under the paraboloid \(z = x^2 y^2\) and above the triangle enclosed by the lines \(y = x, \, x = 0\), and \(x y = 2\) in the \(xy\)plane Solution First examine the region over which we need to set up the double integral and the accompanying paraboloidFind the volume below the paraboloid z =1 x^2 y^2 and above the xyplane Expert Answer 100% (3 ratings) Because this problem deals with parabaloid you are going to want to change it to polar First change z = 1 x^2 y^2 into polar This is done by using the fa view the full answer




Stoke S Theorem S Is The Part Of The Paraboloid Z X 2 Y 2 That Lies Insided The Parabaloid And Cyli Youtube



Http Www Cis Umac Mo Fstitl Calculus12 13 Lecture 07a Pdf



Answered 71 The Solid Bounded By The Paraboloid Bartleby




Se Cylindrical Coordinates To Evaluate The Triple Integral Ex2 Y2 Dv Ex2 Y2dv Where E Is Brainly Com




A Hyperbolic Paraboloid Z X 2 Y 2 Download Scientific Diagram



Solved Consider The Hyperbolic Paraboloid Z X2 Y2 A Drone Is Programmed To Y Along The Surface Of The Hyperbolic Paraboloid The Ight Instrumen Course Hero




Use Polar Coordinates To Find The Volume Of The Given Solid Below The Paraboloid Z 18 2x 2 2y 2 And Above The Xy Plane Homework Help And Answers Slader




Draw The Solid Bounded By The Paraboloid Z 6 X 2 Y 2 And The Plane Z 0 Study Com




Find The Volume Of The Solid Enclosed By The Paraboloid Z 4 X 2 Homeworklib



Http Macs Citadel Edu Zhangli Courses Taught Fall16 Courses Math231 Quiz15 Key Pdf




How To Find The Volume Of A Solid Region Bounded By Paraboloid Z 4 X 2 2y 2 And The Xy Plane Quora



Www Noahdearmath Com Uploads 2 7 2 9 Mth 254 Lesson Triple Integrals In Cylindrical And Spherical Coordinates Solutions Pdf




Triple Integral In Cylindrical Coordinates Plan And Example Parabaloid And Plane Bounds Youtube




Answered Use Cylindrical Coordinates Evaluate Bartleby
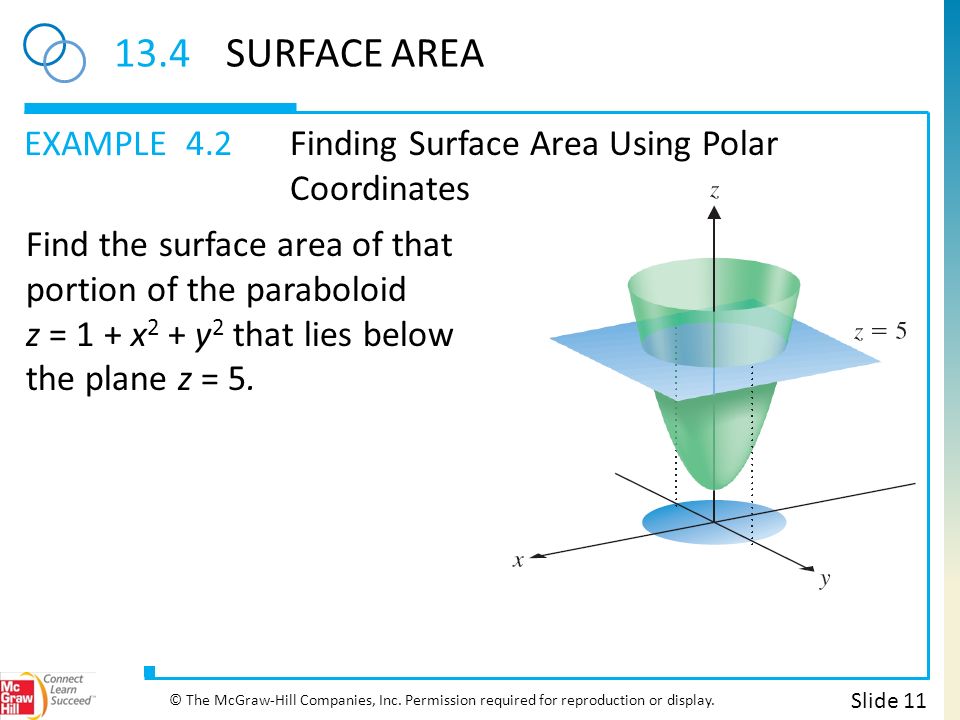



Chapter 13 Multiple Integrals Slide 2 C The Mcgraw Hill Companies Inc Permission Required For Reproduction Or Display 13 1double Integrals 13 2area Ppt Download




Find The Volume Of The Solid Bounded By The Paraboloid Z X 2 Y 2 And The Plane Z 9 In Rectangular Coordinates Study Com




Find The Volume Of The Solid Bounded By The Plane Z 0 And The Paraboloid Z 1 X 2 Y 2 Use A Double Integral And Polar Coordinates Include A Sketch Of The Three Dimensional Paraboloid As



Surface Area




Answered 4 Let S Be The Portion Of The Bartleby




Contour Plots Of The Elliptic Paraboloid Z 1 X 2 2 2 Y 2 In The Download Scientific Diagram



Www Noahdearmath Com Uploads 2 7 2 9 Mth 254 Lesson Triple Integrals In Cylindrical And Spherical Coordinates Solutions Pdf



1




Find The Volume Of The Solid Bounded By The Plane Z 0 And The Paraboloid Z 1 X 2 Y 2 Use A Double Integral And Polar Coordinates Study Com



Volume Of A Solid With A Known Cross Section




Elliptic Paraboloid X 2 Y 2 Z 2 0 Download Scientific Diagram
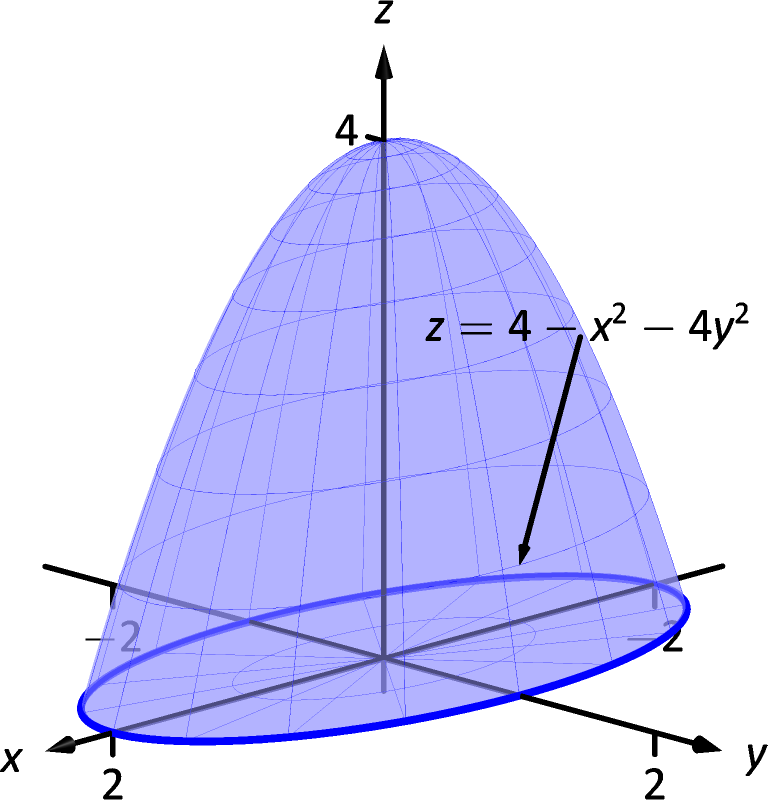



15 5 Parameterized Surfaces And Surface Area Chapter 15 Vector Analysis Part Calculus Iii
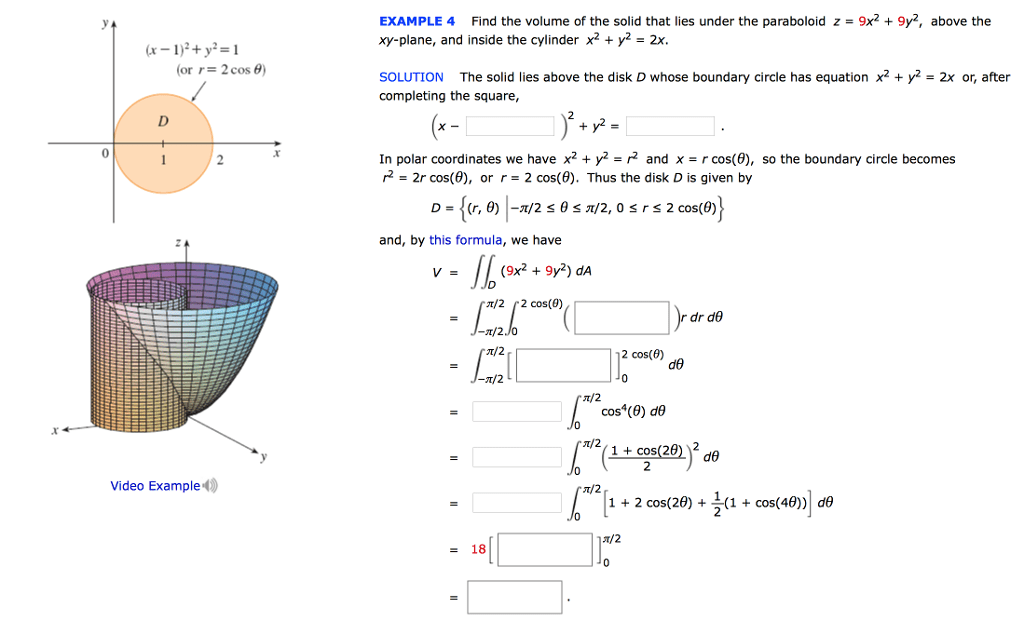



Paraboloid Z 4 X 2 Y 2 Novocom Top
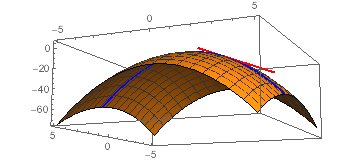



The Paraboloid Z 6 X X 2 2y 2 Intersects The Plane X 1 In A Parabola Find Parametric Equations For The Tangent Line To This Parabola At The
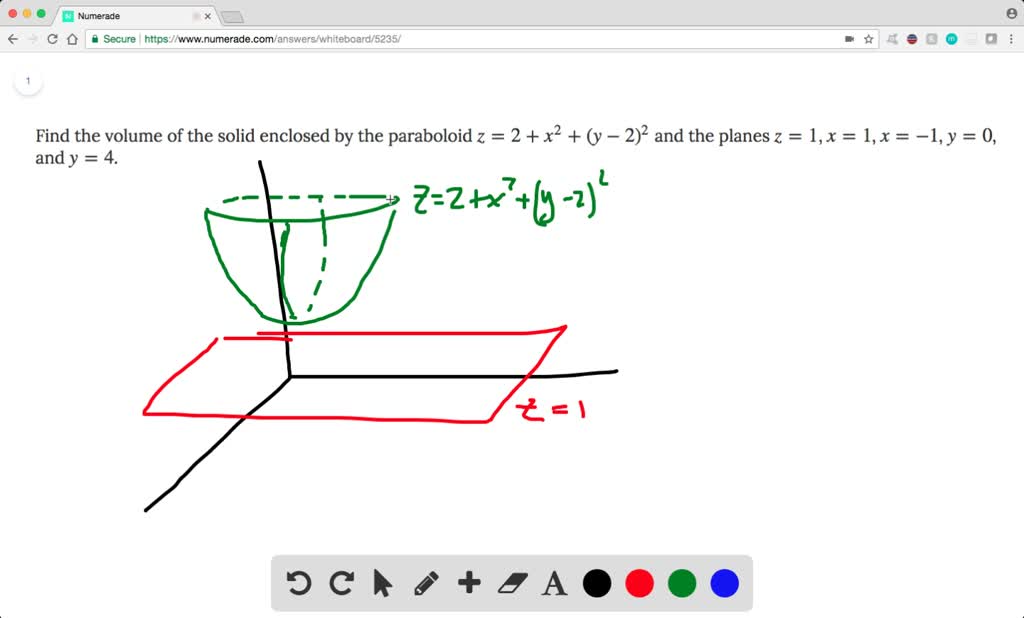



Solved Find The Volume Of The Solid Enclosed By T




Solved A Solid G Is Bounded Above By The Paraboloid Z 1 Chegg Com



Http Www Math Ubc Ca Sjer Math253 S10 Pdf




Answered Find The Volume Of The Solid Enclosed Bartleby



Find The Point On The Paraboloid Z X 2 Y 2 Which Is Closest To The Point 3 6 4 Sarthaks Econnect Largest Online Education Community



Www Ualberta Ca Rjia Math215 Hwks Sol5 Pdf




Find The Volume Of The Solid See How To Solve It At Qanda



1




Section 12 6 Triple Integrals In Cylindrical Coordinates Ppt Download



Find The Surface Area Of The Part Of The Paraboloid Z 5 X 2 Y 2 That Lies Between The Planes Z 0 And Z 1 Mathematics Stack Exchange



2



Http Www Math Washington Edu Sullivan 3263s Au12 Pdf



Www Ualberta Ca Csproat Homework Math 215 Solution 7 Pdf
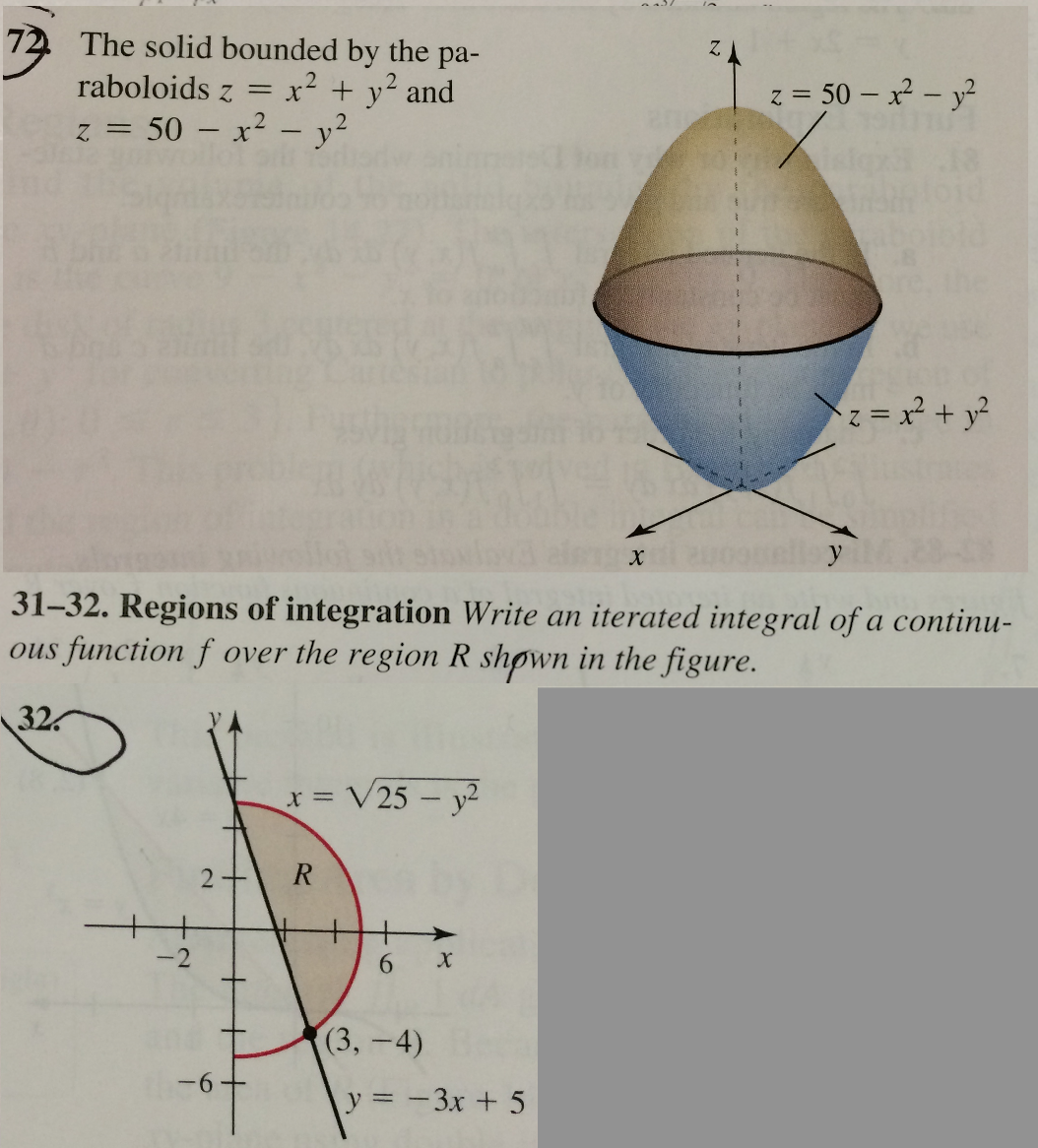



The Solid Bounded By The Paraboloids Z X 2 Y 2 Chegg Com



Http Www Math Ntu Edu Tw Cheng Teaching Calculus Ch16 Pdf



Math 2 Midterm 2



Solved 12 1 1 Points Previous Answersscalcet7 143 094 The Paraboloid Z 1 X X2 2y2 Intersects The Plane X 1 In A Parabola Find Course Hero




Paraboloid Z 4 X 2 Y 2 Novocom Top



X 1 2 Y2 1 For R 2 Coses Example 4 Find The Chegg Com



Solved Find The Area Of The Surface The Part Of



Solved Let S Be The Surface Of The Paraboloid Z 5 X 2 Y 2 Between Planes Z 5 And Z 1 Let C Be The Binding Curve In The Plane Z 1 A Vector Field I Course Hero




Document




Calculus Integration Double Integrals 8 Of 9 Example 7 Finding The Volume Paraboloid Youtube




Paraboloid Z 1 X2 Y2 1 Find The Surface Area Of Chegg Com




Example 2 Find The Volume Of The Solid Bounded By The Chegg Com




Mat 241 Homework Set 10 Mesa Community College Pages 1 4 Flip Pdf Download Fliphtml5
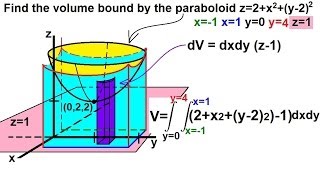



Calculus Integration Double Integrals 8 Of 9 Example 7 Finding The Volume Paraboloid Youtube
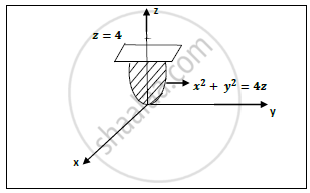



Find The Volume Of The Paraboloid X 2 Y 2 4 Z Cut Off By The Plane 𝒛 𝟒 Applied Mathematics 2 Shaalaa Com



Www Amherst Edu System Files Solution 25practice 25test 253 0 Pdf
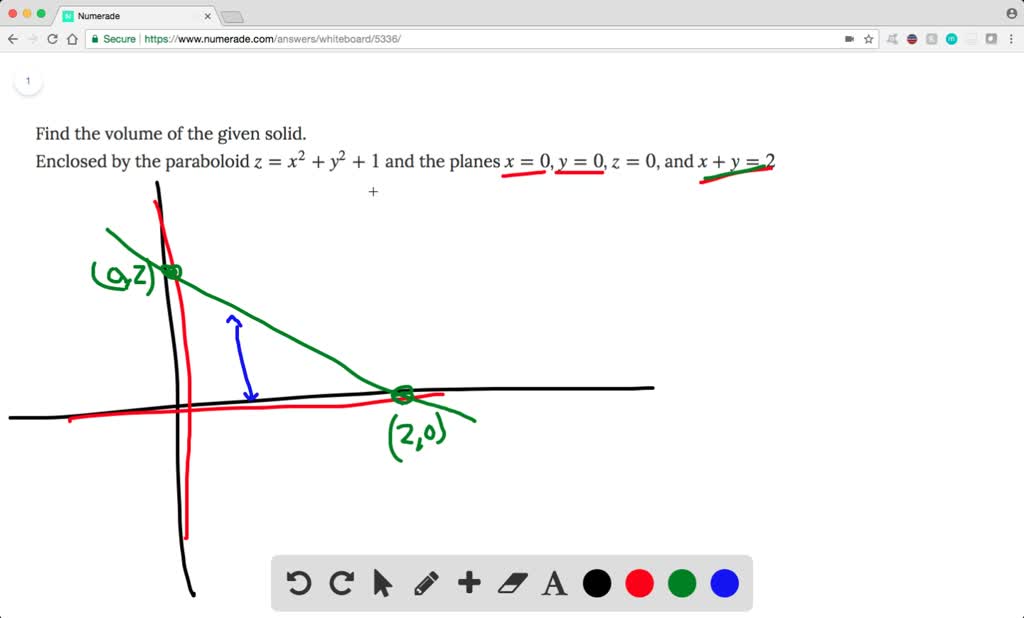



Solved Find The Volume Of The Given Solid Enclos



Http Www Cis Umac Mo Fstitl Calculus12 13 Lecture 07a Pdf




1 Consider The Surface Of Paraboloid Z 1 X2 Y2 Chegg Com
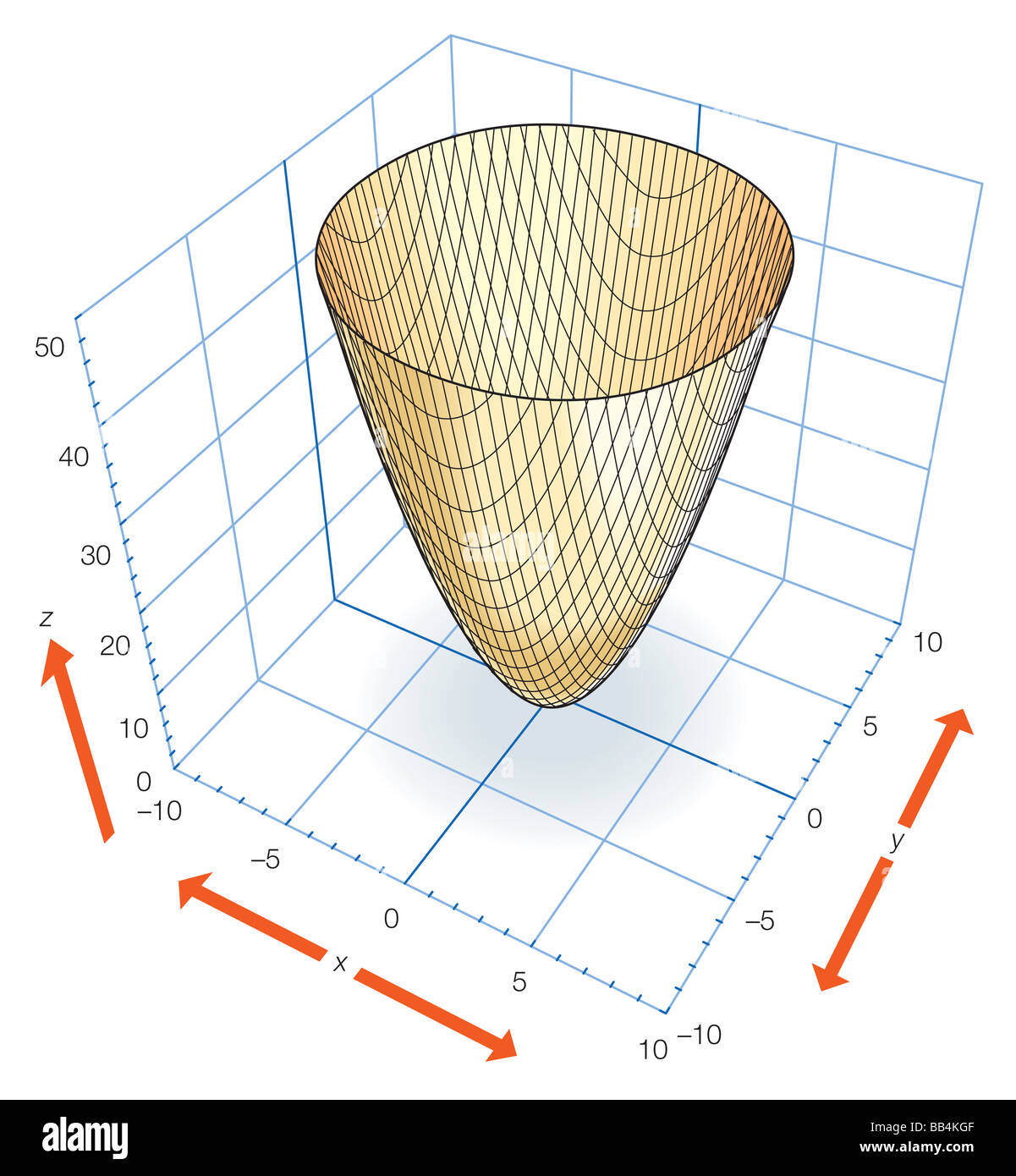



Part Of The Elliptic Paraboloid Z X2 Y2 Which Can Be Generated By Rotating The Parabola Z X2 Or Z Y2 About The Z Axis Stock Photo Alamy




Example 2 Find The Volume Of The Solid Bounded By The Chegg Com



Http Webpages Fc Ul Pt Jaruiz Multivariable Calculus Excerptsmath23b Pdf




Let S1 Be The Part Of The Paraboloid Z 1 X 2 Y Homeworklib




Find An Equation For The Paraboloid Z 4 X 2 Y 2 In Cylindrical Coordinates Type Theta In Your Answer Study Com




Copyright C Cengage Learning All Rights Reserved Ppt Download



Www3 Nd Edu Zxu2 Triple Int16 7 Pdf



Calculation Of Volumes Using Triple Integrals



Tbp Berkeley Edu Exams 40 Download




Example 4 Find The Volume Of The Solid That Lies Under The Paraboloid Z 5x2 5y2 Above The Xy P Homeworklib
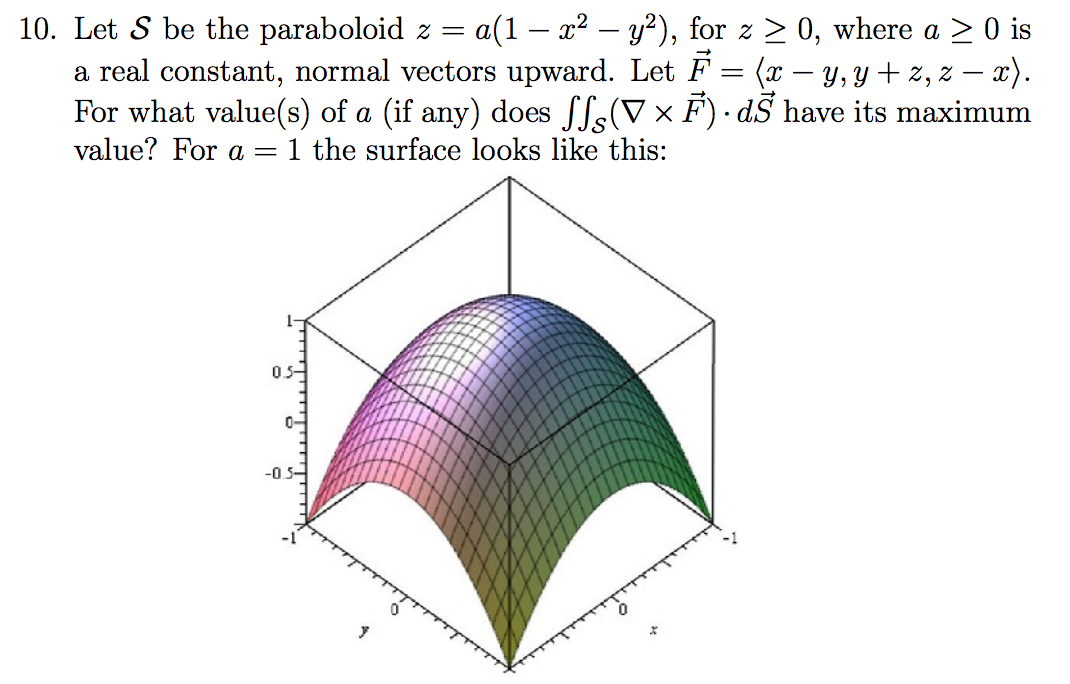



Let S Be The Paraboloid Z A 1 X 2 Y 2 For Z Chegg Com



Www3 Nd Edu Zxu2 Triple Int16 7 Pdf




3 A Consider The Paraboloid Z X2 Y2 Find A Unit Vector Normal To Homeworklib



Www3 Nd Edu Zxu2 Triple Int16 7 Pdf
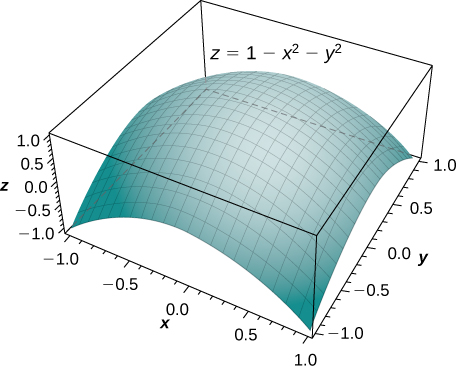



Double Integrals In Polar Coordinates Calculus Volume 3
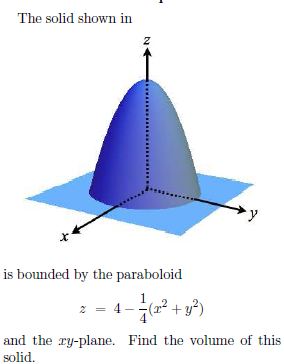



The Solid Shown In Is Bounded By The Paraboloid Z Chegg Com



Solved Use Cylindrical Coordinates Evaluate Iii



1



0 件のコメント:
コメントを投稿